Note
Click here to download the full example code
Calculate DSI-based scalar maps
We show how to calculate two DSI-based scalar maps: return to origin probability (RTOP) [Descoteaux2011] and mean square displacement (MSD) [Wu2007], [Wu2008] on your dataset.
First import the necessary modules:
import numpy as np
import matplotlib.pyplot as plt
from dipy.core.gradients import gradient_table
from dipy.data import get_fnames
from dipy.io.gradients import read_bvals_bvecs
from dipy.io.image import load_nifti
from dipy.reconst.dsi import DiffusionSpectrumModel
Download and get the data filenames for this tutorial.
fraw, fbval, fbvec = get_fnames('taiwan_ntu_dsi')
img contains a nibabel Nifti1Image object (data) and gtab contains a GradientTable object (gradient information e.g. b-values). For example to read the b-values it is possible to write print(gtab.bvals).
Load the raw diffusion data and the affine.
data, affine = load_nifti(fraw)
bvals, bvecs = read_bvals_bvecs(fbval, fbvec)
bvecs[1:] = (bvecs[1:] /
np.sqrt(np.sum(bvecs[1:] * bvecs[1:], axis=1))[:, None])
gtab = gradient_table(bvals, bvecs)
print('data.shape (%d, %d, %d, %d)' % data.shape)
data.shape (96, 96, 60, 203)
Instantiate the Model and apply it to the data.
dsmodel = DiffusionSpectrumModel(gtab, qgrid_size=35, filter_width=18.5)
Let’s just use one slice only from the data.
dataslice = data[30:70, 20:80, data.shape[2] // 2]
Normalize the signal by the b0
dataslice = dataslice / (dataslice[..., 0, None]).astype(float)
Calculate the return to origin probability on the signal that corresponds to the integral of the signal.
print('Calculating... rtop_signal')
rtop_signal = dsmodel.fit(dataslice).rtop_signal()
Calculating... rtop_signal
0%| | 0/2400 [00:00<?, ?it/s]
100%|##########| 2400/2400 [00:00<00:00, 632386.58it/s]
Now we calculate the return to origin probability on the propagator, that corresponds to its central value. By default the propagator is divided by its sum in order to obtain a properly normalized pdf, however this normalization changes the values of RTOP, therefore in order to compare it with the RTOP previously calculated on the signal we turn the normalized parameter to false.
print('Calculating... rtop_pdf')
rtop_pdf = dsmodel.fit(dataslice).rtop_pdf(normalized=False)
Calculating... rtop_pdf
0%| | 0/2400 [00:00<?, ?it/s]
100%|##########| 2400/2400 [00:00<00:00, 649021.90it/s]
In theory, these two measures must be equal, to show that we calculate the mean square error on this two measures.
mse = np.sum((rtop_signal - rtop_pdf) ** 2) / rtop_signal.size
print("mse = %f" % mse)
mse = 0.000000
mse = 0.000000
Leaving the normalized parameter to the default changes the values of the RTOP but not the contrast between the voxels.
print('Calculating... rtop_pdf_norm')
rtop_pdf_norm = dsmodel.fit(dataslice).rtop_pdf()
Calculating... rtop_pdf_norm
0%| | 0/2400 [00:00<?, ?it/s]
100%|##########| 2400/2400 [00:00<00:00, 645815.72it/s]
Let’s calculate the mean square displacement on the normalized propagator.
print('Calculating... msd_norm')
msd_norm = dsmodel.fit(dataslice).msd_discrete()
Calculating... msd_norm
0%| | 0/2400 [00:00<?, ?it/s]
100%|##########| 2400/2400 [00:00<00:00, 636787.04it/s]
Turning the normalized parameter to false makes it possible to calculate the mean square displacement on the propagator without normalization.
print('Calculating... msd')
msd = dsmodel.fit(dataslice).msd_discrete(normalized=False)
Calculating... msd
0%| | 0/2400 [00:00<?, ?it/s]
100%|##########| 2400/2400 [00:00<00:00, 638604.94it/s]
Show the RTOP images and save them in rtop.png.
fig = plt.figure(figsize=(6, 6))
ax1 = fig.add_subplot(2, 2, 1, title='rtop_signal')
ax1.set_axis_off()
ind = ax1.imshow(rtop_signal.T, interpolation='nearest', origin='lower')
plt.colorbar(ind)
ax2 = fig.add_subplot(2, 2, 2, title='rtop_pdf_norm')
ax2.set_axis_off()
ind = ax2.imshow(rtop_pdf_norm.T, interpolation='nearest', origin='lower')
plt.colorbar(ind)
ax3 = fig.add_subplot(2, 2, 3, title='rtop_pdf')
ax3.set_axis_off()
ind = ax3.imshow(rtop_pdf.T, interpolation='nearest', origin='lower')
plt.colorbar(ind)
plt.savefig('rtop.png')
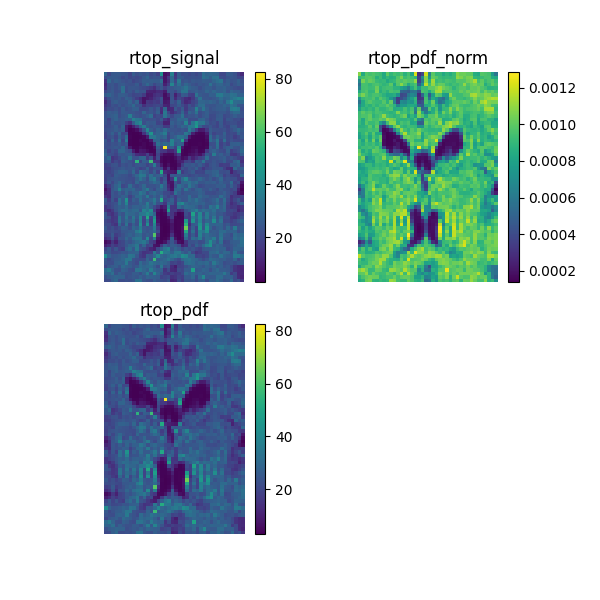

Show the MSD images and save them in msd.png.
fig = plt.figure(figsize=(7, 3))
ax1 = fig.add_subplot(1, 2, 1, title='msd_norm')
ax1.set_axis_off()
ind = ax1.imshow(msd_norm.T, interpolation='nearest', origin='lower')
plt.colorbar(ind)
ax2 = fig.add_subplot(1, 2, 2, title='msd')
ax2.set_axis_off()
ind = ax2.imshow(msd.T, interpolation='nearest', origin='lower')
plt.colorbar(ind)
plt.savefig('msd.png')
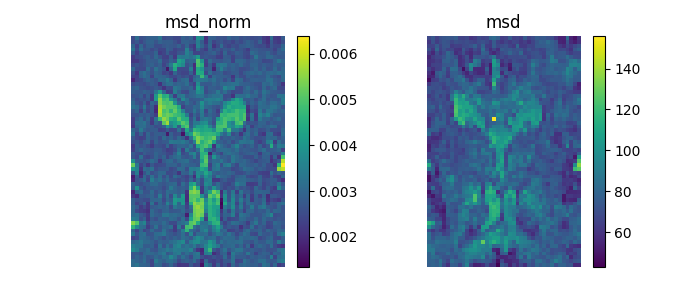

Descoteaux M. et al., “Multiple q-shell diffusion propagator imaging”, Medical Image Analysis, vol 15, no 4, p. 603-621, 2011.
Wu Y. et al., “Hybrid diffusion imaging”, NeuroImage, vol 36, p. 617-629, 2007.
Wu Y. et al., “Computation of Diffusion Function Measures in q-Space Using Magnetic Resonance Hybrid Diffusion Imaging”, IEEE Transactions on Medical Imaging, vol 27, no 6, p. 858-865, 2008.
Total running time of the script: ( 0 minutes 11.310 seconds)